We have a rectangular sheet with length (l) and width (w)
It is also given that length is four times the width,
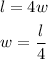
The perimeter of the sheet must be less than 100 inches,
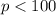
Recall that the perimeter of a rectangular shape is given by
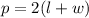
Substitute it into the above inequality

Now substitute the value of w into the above inequality.
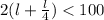
Now let us simplify the above inequality
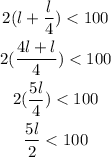
Therefore, the possible lengths of the rectangular sheet are given by the inequality
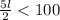
The 2nd option is the correct answer.