Question

Plato classes Consider the graphs of the parent logarithmic function f and transformed function g

Answer 1

To go from function f to function g you dilated f fromthe x-axis in the y direction also known as a vertical stretch.

To find the factor of the vertical stretch you identify the change in y-values for the same x-value; approximate changes:

For x=4

In f y= 2, in g y=4

For x=8

In f y=3, in g y=6

As you can see above the y-values duplicate, then the factor is 2.

The vertical stretch can be written in the next form:

`\begin{gathered} f(x)=logx \\ \\ g(x)=alogx \end{gathered}`

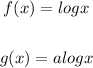
a is the factor of dialtion.

Then, to produce g, function f was vertically stretch by a factor of 2, function g is defined as g(x)=2log(x)