The Solution:
Given:
The first derivative gives:
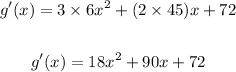
So,
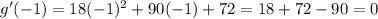
The second derivative gives:
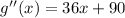
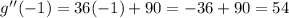
By the second derivative test:

Thus, the function g(x) has a local minimum at x= -1 since the second derivative is greater than zero at x = -1.
At x =-1, the graph og g(x) is concave up.