Question

The Titanic hit an iceberg estimated to be half of it’s mass. Before hitting the iceberg, the Titanic was estimated to be going 22 kts (11.3 m/s). After hitting the iceberg, the Titanic was estimated to be going about 6.0 knots (3.1 m/s). How fast was the iceberg going after the collision? (Assume a head-on collision).

Answer 1

We are given that the Titanic hit an iceberg half of its mass. To determine the velocity of the iceberg after the collision we have to do a balance of momentum:

`m_Tv_(1T)+m_Iv_(1I)=m_Tv_(2T)+m_Iv_(2I)`

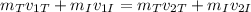
Where:

`\begin{gathered} m_T=\text{ mass of the titanic} \\ v_(1T)=\text{ initial velocity of the titanic} \\ m_I=\text{ mass of the Iceberg} \\ v_(1I)=\text{ initial velocity of the iceberg} \\ v_(2T)=\text{ final velocity of the titanic} \\ v_(2I)=\text{ final velocity of the iceberg} \end{gathered}`

Now, since the iceberg is initially at rest, we have:

`v_(1I)=0`

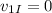
Substituting in the balance of momentum we get:

`\begin{gathered} m_Tv_(1T)+m_I(0)_{}=m_Tv_(2T)+m_Iv_(2I) \\ m_Tv_(1T)=m_Tv_(2T)+m_Iv_(2I) \end{gathered}`

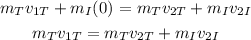
We are given that the mass of the iceberg is half of the mass of the Titanic, therefore, we have:

`m_I=(m_T)/(2)`

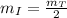
Substituting in the balance of momentum:

`m_Tv_(1T)=m_Tv_(2T)+(m_T)/(2)v_(2I)`

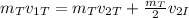
Now, we can cancel out the mass of the Titanic:

`v_(1T)=v_(2T)+(1)/(2)v_(2I)`

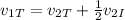
Now we solve for the final velocity of the iceberg. We subtract the final velocity of the Titanic from both sides:

`v_(1T)-v_(2T)=(1)/(2)v_(2I)`

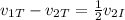
Now we multiply both sides by 2:

`2(v_(1T)-v_(2T))=v_(2I)`

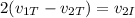
Substituting the values we get:

`2(11.3(m)/(s)-3.1(m)/(s))=v_(2I)`

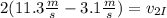
Solving the operations we get:

`16.4(m)/(s)=v_(2I)`

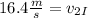
Therefore, the final velocity of the iceberg is 16.4 meters per second.