Question

Graph the following relation. Use the graph to find the domain and range (in interval form) and indicate whetherthe graph is the graph of a function.y = 1/2x -4 Domain: Range: Is it a function? Yes No

Answer 1

Given:

The equation is:

`y=(1)/(2)x-4`

Find-:

The Domain, Range and it is a function or not

Explanation-:

Equation is

`y=(1)/(2)x-4`

The graph of the line is:

At x = 0 value of y,

`\begin{gathered} y=(1)/(2)x-4 \\ \\ x=0 \\ \\ y=(1)/(2)(0)-4 \\ \\ y=-4 \end{gathered}`

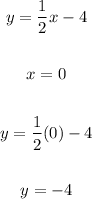
At y = 0 value of x,

`\begin{gathered} y=(1)/(2)x-4 \\ \\ 0=(1)/(2)x-4 \\ \\ 4=(1)/(2)x \\ \\ x=8 \end{gathered}`

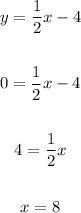
So, line pass through ( 0, -4) and ( 8, 0 )

The graph of the line is:

Domain- The domain of a function is the set of its possible inputs, i.e., the set of input values where for which the function is defined. In the function machine metaphor, the domain is the set of objects that the machine will accept as inputs.

For the line is:

`\begin{gathered} y=(1)/(2)x-4 \\ \\ \text{ Domain }=\text{ All real number} \\ \\ \end{gathered}`

Range-

The range is the difference between the highest and lowest values in a set of numbers.

The output of the function is:

`\text{ Range }=(-\infty,\infty)`

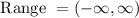
It is a function or not

Function, in mathematics, an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable).

`\begin{gathered} y=(1)/(2)x-4 \\ \end{gathered}`

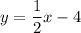
So, it is a function.