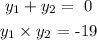Question

Use vietas formula to find the sum of the roots of the equation

Answer 1

y1 + y2 = 0

y1*y2 = -19

Step-by-step explanation:

The equation: y^2 - 19 = 0

Using Vieta's formula for equation in the form:

ax^2 + bx + c = 0

sum of roots = -b/a

Product of roots = c/a

Comparing the equation above with the equation in the question:

y^2 + 0x -19 = 0

coefficent of y^2 = a = 1

coefficient of x = b = 0

The constant = c = -19

`\begin{gathered} sumofroots=y_1+y_2 \\ \text{sum of roots = }(-0)/(1)\text{ = 0} \\ sum\text{ of roots = }0 \end{gathered}`

`\begin{gathered} Productofroots=y_1* y_{2\text{ }}\text{= }(c)/(a) \\ \text{Product of roots = }(-19)/(1) \\ \text{product of root = -19} \end{gathered}`

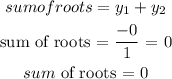
Hence:

`\begin{gathered} y_1+y_2=\text{ 0} \\ y_1* y_2\text{ = -19} \end{gathered}`