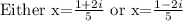• The value of the discriminant ,D= -16
,
• The solution to the quadratic equation is
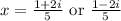
Step - by - Step Explanation
What to find?
• The discriminant d= b² - 4ac
,
• The solution to the quadratic equation.
Given:
5x² - 2x + 1=0
Comparing the given equation with the general form of the quadratic equation ax² + bx + c=0
a=5 b=-2 and c=1
Uisng the quadratic formula to solve;
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/pxvjqgmokhpuiark1x2l.png)
The discriminant D=b² - 4ac
Substitute the values into the discriminant formula and simplify.
D = (-2)² - 4(5)(1)
D = 4 - 20
D = -16
We can now proceed to find the solution of the quadratic equation by substituting into the quadratic formula;
![x=\frac{-(-2)\pm\sqrt[]{-16}}{2(5)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/sn05wcmud5ckw2rwxjj7.png)
Note that:
√-1 = i
![x=\frac{2\pm\sqrt[]{16*-1}}{10}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/tx0x76rxgkwshyg7yqkz.png)
![x=\frac{2\pm\sqrt[]{16}*\sqrt[]{-1}}{10}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/yr7as2piokhhx1k4apyu.png)
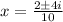
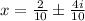
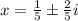
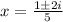
That is;