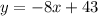Question

Consider the line y=-8x+7

Answer 1

If we have an equation of the form

`y=mx+b`

then the equation of the perpendicular line is given by

`y=-(1)/(m)x+c`

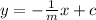
Now, keeping that in mind, the equation of the perpendicular line to y =-8x+7 is

`y=(1)/(8)x+c`

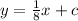
We find c by using the fact that this perpendicular line passes through (-6, -5)

Putting in x = -6 and y = -5 gives

`-5=(1)/(8)(-6)+c`
`-5-(3)/(4)=c`
`c=-(23)/(4)`

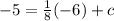
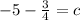
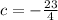
Hence, the equation of the perpendicular line is

`y=-(1)/(8)x-(23)/(4)`

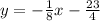
The equation of the parallel line is

`y=-8x+b`

We find b using the point (-6, -5). Putting tn x = -6 and y = -5 gives

`-5=-8(-6)+b`
`b=43`

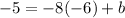
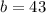
Hence, the equation of the parallel line is

`y=-8x+43`