Question

The length of a rectangular box is 9 inches shorter than twice the width (x).The height is 4 inches.Which is the width (x) when the volume (y) is 1064 cubic inches?

Answer 1

The statement "the length is 9 inches shorter than twice the width" can be expressed as

`l=2w-9`

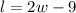
We know the height is 4 inches long, and the volume is 1,064 cubic inches.

The volume of a rectangular box is

`V=w\cdot l\cdot h`

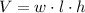
Where w is x. Let's replace each given information.

`1064=x\cdot(2x-9)\cdot4`

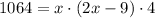
Now, we solve for x.

`\begin{gathered} 1064=(2x^2-9x)\cdot4 \\ (1064)/(4)=2x^2-9x \\ 266=2x^2-9x \\ 2x^2-9x-266=0 \end{gathered}`

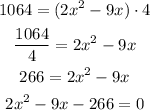
Where a = 2, b = -9, and c = -266. We use the quadratic formula to find the solutions.

`\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{-(-9)\pm\sqrt[]{(-9)^2-4(2)(-266)}}{2(2)} \\ x_(1,2)=\frac{9\pm\sqrt[]{81+2128}}{4}=\frac{9\pm\sqrt[]{2209}}{4}=(9\pm47)/(4) \\ x_1=(9+47)/(4)=(56)/(4)=14 \\ x_2=(9-47)/(4)=(-38)/(4)=-9.5 \end{gathered}`

However, the positive number is the only one that makes sense to the problem since distances can't be negative.

Therefore, the right answer is 14 inches.