Question

What is the answer to this solution? solve for all possible values of x.

Answer 1

Step-by-step explanation

To solve this equation, first, square both sides of the equation,

`(\sqrt[]{25-3x})^2=(x-9)^2`

Simplify the square root with the exponent and expand the binomial squared on the right side of the equation,

`25-3x=x^2-18x+81`

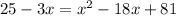
Then, subtract 25 from both sides and add 3x to both sides,

`\begin{gathered} 25-25-3x+3x=x^2-18x+3x+81-25 \\ \\ 0=x^2-15x+56 \end{gathered}`

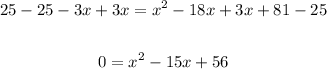
This is a quadratic equation that we can solve using the quadratic formula,

`\begin{gathered} if\text{ }ax^2+bc+c=0 \\ then\text{ }x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}`

In this case, the coefficients are a = 1, b = -15 and c = 56,