Question

Of all the yoga students in a particular area, 20% study with Patrick and 80% study with Carl. We also know that 8% of the yoga students study with Patrick and are female, while 66% of the students study with Carl and are female. What is the probability that a randomly selected yoga student is female, given that the person studies yoga with Carl?

A) .35
B) .56
C) .69
D) .83

Answer 1

Option D - 0.83

Explanation:

Given : Of all the yoga students in a particular area, 20% study with Patrick and 80% study with Carl. We also know that 8% of the yoga students study with Patrick and are female, while 66% of the students study with Carl and are female.

To find : What is the probability that a randomly selected yoga student is female, given that the person studies yoga with Carl?

Solution :

Let p- Patrick , c-Carl and f-female

So, we have given that ,

`P(p)= 20\%=0.2\\P(c)= 80\%=0.8\\P(p\cap f)= 8\%=0.08\\P(c \cap f)= 66\%=0.66\\`

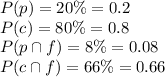
We have to find conditional probability where yoga student is female , given that the person studies yoga with Carl i.e,
`P(f/c)`

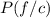
The formula is
`P(f/c)=(P(f\cap c))/(P(c))`

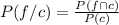
Substitute the values we get,

`P(f/c)=(0.66)/(0.8)`

`P(f/c)=0.825`

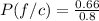
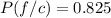
Approximately,
`P(f/c)=0.83`

Therefore, Option D is correct.

The probability that a randomly selected yoga student is female, given that the person studies yoga with Carl is 0.83 or 83%.