Question

For the Christmas Pageant, the drama teacher divided the students into groups of boys and girls. All groups of girls had the same number of students and all groups of boys had the same number of students. For set design and building the drama teacher pulled 3 groups of boys and 2 groups of girls for a total of 71 students. For the pit band the drama teacher pulled 1 group of boys and 4 groups of girls for a total of 77 students. If the drama teacher had 1 group of boys and 1 group of girls left over to be performers, how many performers does the drama teacher have?

Answer 1

Let x be the number of boys in each boy group and let y be the number of girls each girl group have.

We know that the set design crew has two 3 groups of boys and 2 groups of girls and the total number of students is 71, then we have the equation:

`3x+2y=71`

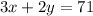
Now, for the pit band we have 1 group of boys and 4 groups of girls and the total number os students is 77. hence we have the equation:

`x+4y=77`

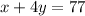
Then we have the system of equations:

`\begin{gathered} 3x+2y=71 \\ x+4y=77 \end{gathered}`

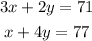
To determine how many students each king of group have we solve the system; to do this we solve the second equation for x:

`x=77-4y`

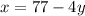
Now we plug this value in the first equation and solve for y:

`\begin{gathered} 3(77-4y)+2y=71 \\ 231-12y+2y=71 \\ -10y=71-231 \\ -10y=-160 \\ y=(-160)/(-10) \\ y=16 \end{gathered}`

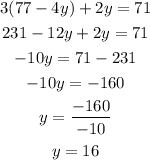
plugging the value of y in the equation for x we have that:

`\begin{gathered} x=77-4(16) \\ x=77-64 \\ x=13 \end{gathered}`

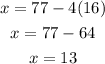
Hence we conclude that each boy group has 13 students and each girl group has 16 students.

Finally the performers crew has one of each kind of group; therefore the performance crew has 29 students.