Question

Define two terms, each containing the variables x and y, with exponents on each. (For example: 10x'y-5) Find the quotient of the two terms. Explain step-by-step how you found the quotient.

Answer 1

We need to define two terms in the form:

`ax^by^c`

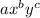
with a, b, and c constants. Then, we need to find the quotient of those terms.

One way to define those terms is by choosing the constants to be, for the first term:

`\begin{gathered} a=6 \\ b=3 \\ c=4 \end{gathered}`

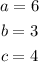
Thus, the first term can be:

`6x^3y^4`

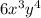
And. for the second term, we could choose, for instance:

`\begin{gathered} a=3 \\ b=2 \\ c=2 \end{gathered}`

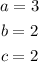
Thus, the second term would be:

`3x^(2)y^(2)`

Now, the quotient of those terms can be found by grouping the terms with the same base and applying the rule:

`(x^i)/(x^j)=x^(i-j)`

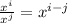
Thus, we obtain:

`(6x^3y^4)/(3x^(2)y^(2))=(6)/(3)\cdot(x^3)/(x^(2))\cdot(y^4)/(y^(2))=2\cdot x^(3-2)\cdot y^(4-2)=2x^(1)y^(2)=2xy^(2)`