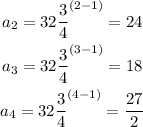Question

I need help answering this practice problem from my calculus prep book

Answer 1

We can use the following rule to write any term of a geometric sequence:

`a_n=a_1r^((n-1))`

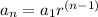
Where a1 is the first term of the sequence and r is the common ratio.

We know that:

`\begin{gathered} a_1=32 \\ a_5=(81)/(8) \end{gathered}`

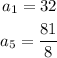
Now we can write the equation:

`(81)/(8)=32r^((5-1))`

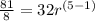
Now we can solve:

`\begin{gathered} (81)/(8\cdot32)=r^4 \\ r=\sqrt[4]{(81)/(256)}=(3)/(4) \end{gathered}`

Now that we know the ratio, we can find any term in the sequence, by using:

`a_n=32(3)/(4)^((n-1))`

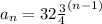
The problem ask us to find a2, a3 and a4:

`\begin{gathered} a_2=32(3)/(4)^((2-1))=24 \\ a_3=32(3)/(4)^((3-1))=18 \\ a_4=32(3)/(4)^((4-1))_{}=(27)/(2) \end{gathered}`