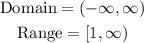Question

The graph of a quadratic function with vertex (3,1) is shown in the figure below.Find the range and the domain.

Answer 1

Observe the given graph carefully.

The curve of a quadratic function is a parabola. The curve is a parabola having concave upwards.

So the vertex will be the lowest point on the parabola.

Given that the vertex of the parabola is,

`(3,1)`

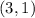
It means that the lowest value that 'y' can take is 1.

It follows that,

`y\ge1`

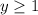
Also, the quadratic function is defined for all real values of 'x'.

It is known that all values of 'x' constitute the domain while all values of 'y' constitute the range of the function.

Therefore, the domain and range of the function are,

`\begin{gathered} \text{Domain}=(-\infty,\infty) \\ \text{Range}=\lbrack1,\infty) \end{gathered}`