If the sequence has a common difference of 4, this means that:
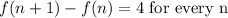
We can use that to find f(2), f(3), etc...
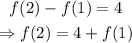
Substitute f(1)=3:

The next term will be given by:
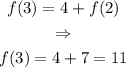
By adding 4 to the previous term, it follows that f(4)=15, f(5)=19, and so on.
The sequence 3, 7, 11, 15, 19 appears in the option C.