Question

A ladder is leaning against annulling so that the distance from the ground to the top of the ladder is 3 feet less than the length of the ladder. Find the length of the ladder if the distance from the bottom of the ladder to the building is 9 feet The lender of the ladder is ?

Answer 1

From the problem we know that:

• x is the length of the ladder,

,

• the top of the ladder is 3 feet less than the length of the ladder,

,

• the distance from the bottom of the ladder to the building is 9 feet.

Adding the data of the problem to the drawing, we have:

We see that the ground, the wall and the ladder forms a right triangle of sides a, b and h, where:

• the hypotenuse is h = x,

,

• one cathetus is a = 9,

,

• the second cathetus is b = x - 3.

Pitagoras Theorem states that:

`h^2=a^2+b^2.`

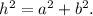
Replacing the values of a, b and h, we have the following equation for x:

`x^2=9^2+(x-3)^2.`

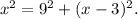
We solve for x the equation:

`\begin{gathered} x^2=81+x^2-2\cdot3\cdot x+3^2, \\ x^2=81+x^2-6x+9, \\ 0=90-6x, \\ 6x=90, \\ x=(90)/(6)=15. \end{gathered}`

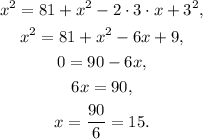
Answer

The length of the ladder is x = 15 feet.