Question

Please make sure you answer with all the steps

Thanks you so much :)

Answer 1

18. (i dont know this one but I know rest )Solve 3x^2-5x+4=0 by using quarartic equation ((-bV(b^2-4ac))/2a) If you put in values for a=3 b=-5 and c=4. You get no answer

19. Solve the quaratic equation for a=-16 b=25 c=3 to get about 1.67447537 seconds for one solution. the other is in -, so that one isn't the answer.

20. when the time is 1, then you can insert the into h(t) by doing h(1)=-16*1^2 +25*1^2 +3 to get 12. that means that the balloon is at 12 feet at one second.

Answer 2

the discriminant tells how many solutions and what type
b^2-4ac is that disccriminant
where you have ax^2+bx+c=0
a=3
b=-5
c=4
discriminant=(-5)^2-4(3)(4)=25-somethingbiggerthan25=negative
since it is negative, you will have 0 real solutions and 2 complex solutions (if you remember quadratic formula, the discriminat is under sqrt sign so if it is negative you get complex roots)

18. 0 real roots

19. hit the ground means height=0
set to zero and solve
0=-16t^2+25t+3
use quadratic fomrula
for equaiton ax^2+bx+c=0
x=
`\frac{-b+/- \sqrt{b^(2)-4ac} }{2a}`

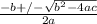
a=-16
b=25
c=3
x=
`\frac{-25+/- \sqrt{25^(2)-4(-16)(3)} }{2(1)}`
x=
`(-25+/- √(625+192) )/(2)`
x=
`(-25+/- √(817) )/(2)`
apxos
x=1.79161 or -26.7916
since x=time, we can't have negative time so
it take 1.79161 seconds

20.
t=1
sub1 for every t
h(1)=-16(1)^2+25(1)+3
h(1)=-16+25+3
h(1)=12

12 feet


18. zero real roots
19. t=1.79161 seconds
20. 12 feet