Question

Let f be defined as shown. If the domain is restricted to {1,0), which statement is true? The inverse of f exists. The inverse of f does not exist.

Answer 1

Step 1 :

In this question, we are given the function f.

If the domain is restricted to {1,0),

We can see clearly that:

`\begin{gathered} f(0\text{) = }9 \\ \text{f (1) = }4 \end{gathered}`

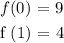
which makes it a one-to-one function.

Step 2 :

A function f is one - to -one if no two elements in the domain of f correspond to the same element in the range of f.

In other words, each x in the domain has exactly one image in the range.

And, no y in the range is the image of more than one x in the domain.

Step 3 :

In fact, only one-to-one functions have an inverse.

If a function is many-to-one the process to reverse it would require many outputs from one input contradicting the definition of a function.

CONCLUSION:

The inverse of f exists.