The equation:
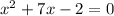
has the values a=1, b=7 and c=-2; hence the discriminant is:
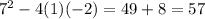
Since the disciminant is positive this means that the equation will have two different solutions.
The solutions can be found using the general formula:
![\begin{gathered} x=\frac{-7\pm\sqrt[]{7^2-4(1)(-2)}}{2(1)} \\ x=\frac{-7\pm\sqrt[]{57}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7bxjvfu69jlh579xtx3v.png)
therefore the solutions are:
![\begin{gathered} x=-(7)/(2)+\frac{\sqrt[]{57}}{2} \\ \text{and} \\ x=-(7)/(2)-\frac{\sqrt[]{57}}{2} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/87b5lnorxh4solgaf7po.png)