Question

For the function given below, find a formula for the riemann sum obtained by dividing the interval [a,b] into n equal subintervals and using the right-hand endpoint for each c subscript k. then take a limit of this sum as n right arrow infinity to calculate the area under the curve over [a,b]. f(x)equals2x over the interval [2,4].

Answer 1

Given

`f(x)=2x,[2,4]`

Find

Area under the curve.

Step-by-step explanation

first , we split interval [2 , 4] into n subintervals of length

`(4-2)/(n)=(2)/(n)`

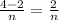
so ,

`[2,4]=[2,2+(2)/(n)]\cup[2+(2)/(n),2+(4)/(n)]\cup[2+(4)/(n),2+(6)/(n)]\cup.....\cup[2+(2(n-1))/(n),4]`

so that the right endpoints are given by the sequence

`x_i=2+(2i)/(n)=(2(n+i))/(n),for\text{ }1\leq i\leq n`

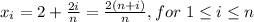
then Riemann sum approximating ,

`\int_2^42xdx=\sum_{i\mathop{=}1}^nf(x_i)(4-2)/(n)=(12n+4)/(n)`

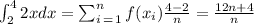
the integral is given exactly as n tends to infinity , for which we get ,

`\int_2^42xdx=\lim_(n\to\infty)((12n+4)/(n))=12`

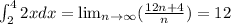
Final Answer

Hence ,

`\int_2^42xdx=12`