Question

Find the unknown measure. Round lengths to the nearest hundredth and angle measures to the nearest degree. Please help

Answer 1

Given:

AR=12 and AP=4.6,

Using Pythagorean theorem to find RP.

`RP^2=AR^2+AP^2`

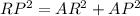
Substitute AR=12 and AP=4.6, we get

`RP^2=12^2+4.6^2^{}`

`RP^2=165.16`

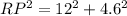
Taking square root on both sides, we get

`RP^{}=\sqrt[]{165.16}=12.8514590611`
`RP=12.85`

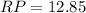
Hence the unknown length is 12.85 units.

Given that angle A=90 degrees.

Using sine law.

`\frac{\text{RP}}{\sin A}=(AR)/(\sin P)=(AP)/(\sin R)`

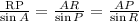
Substitute known values, we get

`(12.85)/(\sin90^o)=(12)/(\sin P)=(4.6)/(\sin R)`

`\text{ Consider }(12.85)/(\sin90^o)=(12)/(\sin P)\text{.}`
`\text{Use }\sin 90^o=1.`

`(12.85)/(1)=(12)/(\sin P)\text{.}`
`\sin P=(12)/(12.85)`

`\sin P=0.93385214007`
`\text{ Use sin }69.04348449=0.93385214007`

`\sin P=\sin 69.04348449`
`P=69`

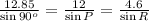
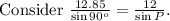
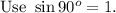
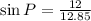
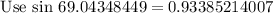
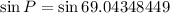
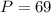
Hence we get

`m\angle P=69^o`

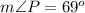
Using the triangle sum property, we get

`m\angle P+m\angle A+m\angle R=180^o`

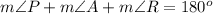
Substitute known values, we get

`69^o+90^o+m\angle R=180^o`

`159^o+m\angle R=180^o`

`m\angle R=180^o-159^o`

`m\angle R=21^o`

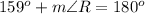
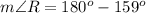
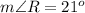
Hence we get unknown angels

`m\angle R=21^o`

`m\angle P=69^o`

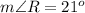
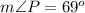
The unknown length is 12.85 units.