Question

1. Calculate the variance of the set of data to two decimal places.{1,2,4,4,5,6,6}a. 22b. 4c.3.14d. 1/7e.2

Answer 1

`3.14`

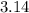
Step-by-step explanation

To find the variance of the data set, we have to apply the formula:

`s^2=\frac{\sum ^{}_{}(x_i-\mu)^2_{}}{n}`

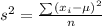
where xi = term in the data set

μ = mean

n = sample size

This means that first, we have to find the mean of the data set and subtract it from each term in the data set.

The mean of the data set is:

`\begin{gathered} \mu=(1+2+4+4+5+6+6)/(7) \\ \mu=(28)/(7) \\ \mu=4 \end{gathered}`

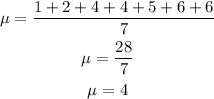
The table below shows the difference between each data set and the mean:

This implies that:

`\begin{gathered} \sum ^{}_{}(x_i-\mu)^2=(-3)^2+(-2)^2+(0)^2+(0)^2+(1)^2+(2)^2+(2)^2 \\ \sum ^{}_{}(x_i-\mu)^2=9+4+0+0+1+4+4 \\ \sum ^{}_{}(x_i-\mu)^2=22 \end{gathered}`

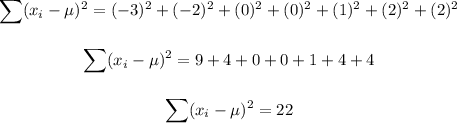
Therefore, the variance is:

`\begin{gathered} s^2=(22)/(7) \\ s^2=(22)/(7) \\ s^2=3.14 \end{gathered}`