Question

The function f(x) = 2x - 33.02 + 1682 + 10 has one local minimum and one local maximum. Use agraph of the function to estimate these local extrema.This function has a local minimum at x = ?with output value =?and a local maximum at x = ?with output value = ?

Answer 1

We have that the local maximum is 282 at x = 4, this means that this function has a local maximum at x = 4 with output value 282 because

`\begin{gathered} 2(4)^3-33(4)^2+168(4)+10=2\cdot(64)-33(16)+672+10 \\ =128-528+682 \\ =282 \end{gathered}`

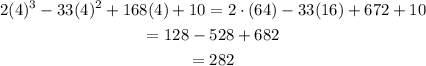
this function has a local minimum at x= 7 with output value 255

`\begin{gathered} 2(7)^3-33(7)^2+168(7)+10=2\cdot(343)-33(49)+1176+10 \\ =686-1617+1176+10 \\ =255 \end{gathered}`

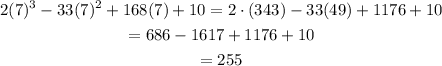
We have that the graph is not easy to see in any scale