Question

A satellite with a mass of 100 kg fires its engines to increase velocity, therebyincreasing the size of its orbit about Earth. As a result, it moves from acircular orbit of radius 7.5 x 10^6m to an orbit of radius 7.7 x 10^6 m. What isthe approximate change in gravitational force from Earth as a result of thischange in the satellite's orbit? (Recall that Earth has a mass of 5.97 x 10^24 kgand G = 6.67 x 10^-11 N•m2/kg2.)

Answer 1

Given,

The mass of the satellite, m=100 kg

The radius of the initial orbit, r=7.5×10⁶ m

The radius of the final orbit of the satellite, R=7.7×10⁶ m

The mass of the earth, M=5.97 x 10²⁴ kg

The gravitational constant, G= 6.67 x 10⁻¹¹ Nm²/kg²

From Newton's universal law of gravitation, the gravitational force on the satellite when it is in the initial orbit is given as

`F_r=\frac{\text{GMm}}{r^2}`

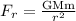
On substituting the known values in the above equation,

`\begin{gathered} F_r=(6.67*10^(-11)*5.97*10^(24)*100)/((7.5*10^6)^2) \\ =707.91\text{ N} \end{gathered}`

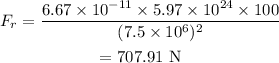
The gravitational force on the satellite, when it is on its final orbit is given by,

`F_R=\frac{\text{GMm}}{R^2}`

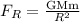
On substituting the known values in the above equation,

`\begin{gathered} F_R=(6.67*10^(-11)*5.97*10^(24)*100)/((7.7*10^6)^2) \\ =671.61\text{ N} \end{gathered}`

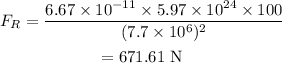
The change in the force is given by,

`\Delta F=F_r-F_R`

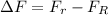
On substituting the known values,

`\begin{gathered} \Delta F=707.91-671.61 \\ =36.3\text{ N} \end{gathered}`

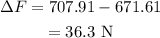
Thus the gravitational force from the Earth decreases by 36.3 N after the satellite changes its orbit.