Question

Carlos is a boat dealer who bought a sailboat for $13,400 and then sold it for $14,600. what percent was his markup on the boat? the percent markup was ____%round to one decimal place as needed.

Answer 1

The percent markup is: 9.0%

SOLUTION

Problem Statement

The question tells us a boat dealer bought a sailboat for $13,400 and sold it for $14600. We are asked to find the percent markup on the boat.

Method

In order to solve this question, we need to understand the meaning of percentage markup.

Definition:

A percentage markup is a profit from selling a good or service, which is a percentage of the cost.

Thus, the selling price of a sailboat is equal to the cost price of the sailboat plus a percentage of the cost price (i.e. markup)

`\begin{gathered} \text{If selling price = SP and cost price = CP} \\ \text{Thus, we have:} \\ SP=CP+CP* X \\ \text{where,} \\ X=\text{markup} \end{gathered}`

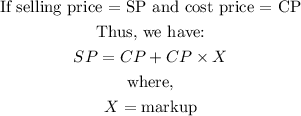
Implementation

Thus, we can find the markup using the formula given above.

`\begin{gathered} SP=14600 \\ CP=13400 \\ \text{Applying the formula:} \\ 14600=13400+13400* X \\ \text{subtract 13400 from both sides} \\ 14600-13400=13400-13400+13400X \\ 1200=13400X \\ \text{Divide both sides by 13400} \\ \\ (1200)/(13400)=(13400X)/(13400) \\ \\ \therefore X=0.0895 \end{gathered}`

Thus, the markup percentage is gotten by just multiplying the value of X by 100 %

Percent Markup is:

`\begin{gathered} X\text{ \%= }0.0895*100 \\ X\text{ \% =8.9552 \%} \\ \\ \therefore\text{Percent Markup }\approx9.0\text{ \%} \end{gathered}`

Final Answer

The percent markup is: 9.0%