Question

A rectangle with area 126 square inches has a length that is three less than three times the width. Find the length and the width of the rectangle.The length is _ inches and the width is_ inches

Answer 1

Let x be the width of the rectangle.

We know that the length of the rectangle is three less that three times its width, this can be express as:

`3x-3`

Now, the area of a rectangle is:

`A=lw`

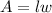
Plugging the value of the area and the expression for the width and lenght we have the equations:

`x(3x-3)=126`

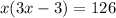
Solving for x we have:

`\begin{gathered} x(3x-3)=126 \\ 3x^2-3x-126=0 \\ x^2-x-42=0 \\ (x-7)(x+6)=0 \\ \text{then } \\ x=7 \\ \text{ or} \\ x=-6 \end{gathered}`

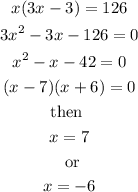
Since a distance is always positive we conclude that x=7.

Now that we know the value of x we plug it in the expression for the length, then we have:

`3(7)-3=21-3=18`

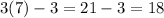
Therefore the lenght is 18 inches and the width is 7 inches.