Question

A body fell freely from a height (h) then it reached the ground with velocity (v), if it fell from height (9h), so it reach the ground with velocity =

Answer 1

Given data:

* The height of the body is H = 9h.

* The initial velocity of the body is u = 0 m/s.

Solution:

In the free fall, the only force that acts on the body is the force of gravity.

By the kinematics equation (for the motion of a body in the vertical direction), the final velocity of the body just before hitting the ground is,

`v^2-u^2=2gH`

where g is the acceleration due to gravity,

If the body falls from the height of h, then the velocity with which the body reaches the ground is v. Thus, above equation of motion becomes,

`\begin{gathered} v^2-0=2gh \\ v^2=2\text{gh} \\ h=(v^2)/(2g) \end{gathered}`

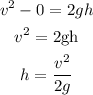
If the body falls 9h height, the final velocity of the body is,

`\begin{gathered} v^2_f-v^2_i=2g(9h) \\ v^2_f-0=18gh \\ v^2_f=18gh \end{gathered}`

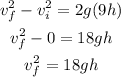
where v_f is the final velocity, v_i is the initial velocity,

By substituting the value of h,

`\begin{gathered} v^2_f=18g*(v^2)/(2g) \\ v^2_f=9v^2 \\ v_f=3v \end{gathered}`

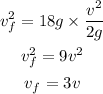
Thus, the final velocity of the body is 3v.