Question

Find directrix of the parabola with vertex (-2,3) and focus (-2,1)

Answer 1

The directrix of the parabola is a line perpendicular to the axis of symmetry and does not touch the parabola.

The vertex of any parabola is equidistant to the focus and the directrix of the parabola, which means that the vertex is at an equal distance between them.

If the vertex is at point (-2,3) and the focus is at point (-2,1), then the directrix must be a line at an equal distance from the vertex but in the opposite direction.

If you graph both points:

Since the focus of the parabolas is "below" the vertex, then you can expect the directrix to be "above" it.

First, calculate the vertical distance between the vertex and the focus. To do so, you have to calculate the difference between the y-coordinates between both points:

`\begin{gathered} d_y=y_(vertex)-y_(focus) \\ d_y=3-1 \\ d_y=2 \end{gathered}`

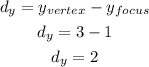
Next, add this distance to the y-coordinate of the vertex, since the directrix is a horizontal line, its equation will be equal to the result of the sum:

`\begin{gathered} directrix:\text{ }y=y_(vertex)+d_y \\ directrix:\text{ }y=3+2 \\ directrix:\text{ }y=5 \end{gathered}`

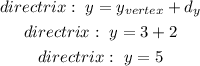
The directrix of the parabola is y= 5