Answer: x^2 - 25
Step-by-step explanation:
Here is a tip/ shortcut to multiplying binomials in the (a + b)(a - b) format.
The only things you have to look for is the factor of a * a and the factor of b * b.
The reason being, a * -b and b * a cancel each other out no matter what.
For example
1. (x + 5)(x - 5) Multiply
 by
by
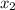
x * x =

2. (x + 5)(x - 5) Multiply
 by -5 in the second binomial
by -5 in the second binomial
x * -5 = -5x
3. (x + 5)(x - 5) Multiply 5 in the first binomial to
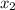
5 * x = 5x
4. (x + 5)(x - 5) Multiply 5 in the first binomial to -5 in the second binomial
5 * -5 = -25
5. Now that you have all of your answers, write your equation, in order, to look like this.
 - 5x + 5x - 25
- 5x + 5x - 25
6. -5x and 5x cancel each other out when combining like terms so you're left with.
 - 25
- 25
In the end, steps 2, 3, 5, and 6. can be taken out by doing this.
Just multiply
 by
by
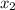 to get
to get

Then just multiply 5 in the first binomial to -5 in the second binomial to get -25
Then write your answer.
 - 25
- 25
This works because there is no need for steps 2,3,5, and 6 since they lead to the same outcome from doing steps 1 and 4.