Question

Solve each equation by completing the square. 3x^2–21=18x.

Answer 1

x = 7 and x = -1

Step-by-step explanation:

The initial equation is:

3x²-21=18x

So, let move the terms with x to one side and the constant terms to the other side as:

3x² - 18x = 21

Now, we can divide by 3:

`\begin{gathered} (3x^2-18x)/(3)=(21)/(3) \\ x^2-6x=7 \end{gathered}`

Now, to complete the square, we need to find a value that is equal to the square of the half of -6, the number beside the x, so the value is:

`((-6)/(2))^2=(-3)^2=9`

Then, we add 9 to both sides of the equation as:

`\begin{gathered} x^2-6x+9=7+9 \\ (x-3)^2=16 \end{gathered}`

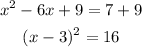
So, solving for x, we get:

`\begin{gathered} \sqrt[]{(x-3)^2}=\sqrt[]{16} \\ x-3=4\to x=4+3=7 \\ or \\ x-3=-4\to x=-4+3=-1 \end{gathered}`

Therefore, the solutions are x = 7 and x = -1