Question

What is the simplest form of the equation
`(4)/(5)n - (1)/(5) = (2)/(5 )`?

Answer 1

`(4)/(5)n\text{ - }(1)/(5)\text{ = }(2)/(5)n`

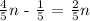
In order to simplify this equation we first need to calculate the LCM between the fractions on the left side. Since the denominator is the same number, the LCM will be that number aswell.

`\frac{4n\text{ - 1}}{5}\text{ = }(2)/(5)n`

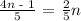
We now need to cross multiply the fractions, multiplying the numerator of each fraction by the denominator of the other one.

`(4n\text{ -1)}\cdot5\text{ = 5}\cdot2n`

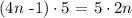
Since there is a "5" multiplying both sides they cancel each other.

`4n\text{ - 1 = 2n}`

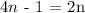
We now need to isolate the "n" on the left side of the equation.

`\begin{gathered} 4n\text{ - 2n = 1} \\ 2n\text{ = 1} \\ n\text{ = }(1)/(2) \end{gathered}`

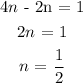
The simplest form of the equation is n = 1/2.