1 Answer

Medy · Answer 1 · 2023-03-25T14:55:28+0000

Solution:

The equation of a line passing through a point is expressed as

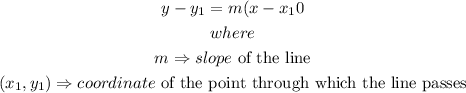
$\begin{gathered} y-y_1=m(x-x_10 \\ where \\ m\Rightarrow slope\text{ of the line} \\ (x_1,y_1)\Rightarrow coordinate\text{ of the point through which the line passes} \end{gathered}$

Given that the line has a slope of 3 and passes through the point (5, 5).

This implies that by substitution, we have

$\begin{gathered} y-5=3(x-5) \\ add\text{ 5 to both sides,} \\ y-5+5=3(x-5)+5 \\ \Rightarrow y=3(x-5)+5 \\ open\text{ parentheeses,} \\ y=3x-15+5 \\ \Rightarrow y=3x-10 \end{gathered}$

Thus, to plot the graph of the above line equation, we solve for y for various values of x.

Thus,

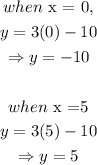
$\begin{gathered} when\text{ x = 0,} \\ y=3(0)-10 \\ \Rightarrow y=-10 \\ \\ when\text{ x =5} \\ y=3(5)-10 \\ \Rightarrow y=5 \end{gathered}$

By plotting the x and y values as points (x,y) on a cartesian graph, we have:

Graph the line with slope 3 passing through the point 5,5-example-1

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions