For this problem we were given a logaritmic function of the type:
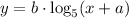
And its graph. From that we need to determine the values of "b" and "a".
From the graph we can notice two important points (6,1) and (2,0). If we replace the coordinates for these two points on the expression for the function, we can determine the values of b and a. This is done below:
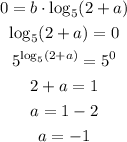
From the first point, we can conclude that "a" is equal to -1. From that, we can find the value of b using the second point:
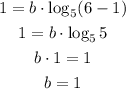
The value for a is -1.
The value for b is 1.