A certain skincare company's profit in millions of dollars, P(t) is modelled by;
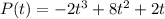
where t represents the number of quantity of skincare items produced, in thousands.
Today, the company produces 4 thousand products for a profit of $8 million.
Mathematically,

Thus, we would find the other quantity that gives same profit with the equation;
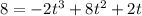
Simplifying further, we have;
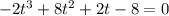
From the previous statement,

is a factor. Thus, we have;
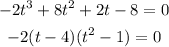
Hence, the other quantity of product would be;
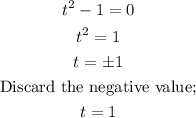
CORRECT OPTION: 1 thousand