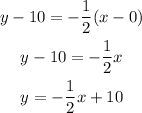The y-intercept of 10 means a point (0,10) on the line.
We already have the point (2,9), so let's find the slope:
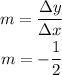
Now, we'll use the value of the slope to calculate k:
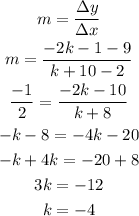
Now for the equation, we'll use the point (2,9)
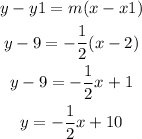
We could also consider we have the y-intercept, which is 10. So, b=10.
Using slope-intercept form, we'll have
y = -1/2m +10