Question

Can someone please help with this question for math, thank you!

Answer 1

The continous exponential growth model has the form:

`P=P_0e^(rt)`

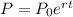
where Po is the starting population, P is the total population after time t, r is the rate growth, t is the time and e is Euler's number. In our case, r = 0.078, P is 2Po and we need to find the time t. By substituting these values, we get

`2P_0=P_0e^{0.078\text{ t}}`

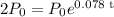
By moving the initial population Po to the left hand side, we get

`(2P_0)/(P_0)=e^{0.078\text{ t}}`

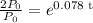
so we can cancel out Po and get

`2=e^{0.078\text{ t}}`

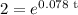
Now, by applying natural logarithm in both sides, we have

`\ln 2=\ln e^{0.078\text{ t}}`

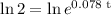
since natural logarithm is the inverse of the exponential function , we get

`\ln 2=0.078t`

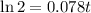
then, by moving the coefficient of t to the left hand side,we obtain

`(\ln 2)/(0.078)=t`

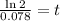
since ln2 is 0.693m, we have

`t=(0.693)/(0.078)`

finally, the time is

`t=8.886\text{ hours}`

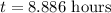
Then, by rounding to the nearest hundredth, the answer is 8.89 hours