Write out the formula of Probability
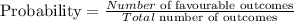
Total number of marbles= total number of red marbles plus the total number of blue marbles.
Total number of marbles= 4+6= 10 marbles.
We were the two different marbles were picked and replaced randomly. So let us get the probability of picking a red marble.
Doubling the probability of pulling a red marble out on the first try is not correct, it will be shown why that is not correct shortly below.
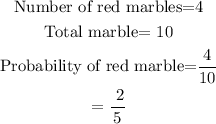

Therefore, the probability of pulling a red marble and also another red marble will result to:

But if you just double the red marble on your first try, you will have:
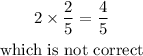
From the calculations done above you can see doubling it is not correct.