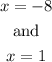Question

3x^2+25x+8__________x^2+7x-8Find the horizontal asymptote or explain why there is nonefind the veriticle asymptote(s) or explain why there is none

Answer 1

The horizontal asymptote for the function is;

`y=3`

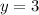
The vertical assyptote for the given function is;

`\begin{gathered} x=-8 \\ \text{and} \\ x=1 \end{gathered}`

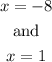
Step-by-step explanation:

Given the function;

`(3x^2+25x+8)/(x^2+7x-8)`

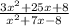
To get the horizontal asymptote, we need to compare the degree of the denominator and the numerator. For the given expression, the degree of the numerator and the denominator are both 2.

So, horizontal asymptote will be equal to the ratio/fraction of the leading coefficient of the expression.

`\begin{gathered} y=(3)/(1) \\ y=3 \end{gathered}`

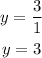
Therefore, the horizontal asymptote for the function is;

`y=3`

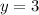
For the vertical asymptote, we need to equate the denominator to zero and solve for x;

`\begin{gathered} x^2+7x-8=0 \\ x^2+8x-x-8=0 \\ x(x+8)-1(x+8)=0 \\ (x+8)(x-1)=0 \\ x=-8 \\ or \\ x=1 \end{gathered}`

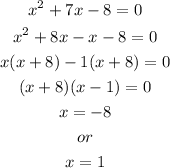
Therefore, the vertical assyptote for the given function is;

`\begin{gathered} x=-8 \\ \text{and} \\ x=1 \end{gathered}`