Question

Find the dimensions of the crate that will minimize the total cost of material

Answer 1

Let's say that the rectangular shipping crate with a square base has the dimensions:

`a* a* b`

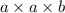
The volume of such a shipping crate is:

`V=a\cdot a\cdot b=a^2\cdot b`

Additionally, the lateral sides have an area of:

`A_L=a\cdot b`

For the base and the top:

`A_B=A_T=a^2`

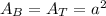
The cost of the material is $7 per square foot for the base and $2 per square foot for the top and the sides. Then, the total cost C will be:

`\begin{gathered} C=2\cdot4\cdot A_L+7\cdot A_B+2\cdot A_T=8A_L+9A_B \\ C=8a\cdot b+9a^2 \end{gathered}`

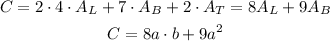
Because there are 4 sides, one base, and one top, and the areas of the base and the top are equal. We know that the volume is a fixed value, then:

`a^2\cdot b=1152\Rightarrow b=(1152)/(a^2)`

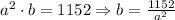
Using this result in the expression of the cost:

`C=8\cdot a\cdot(1152)/(a^2)+9a^2=(9216)/(a)+9a^2`

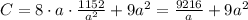
Now, to find the minimum cost, we take the derivative of C with respect to a:

`(dC)/(da)=-(9216)/(a^2)+18a`

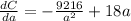
The minimum is obtained by solving the equation dC/da = 0:

`\begin{gathered} -(9216)/(a^2)+18a=0 \\ 18a=(9216)/(a^2) \\ a^3=(9216)/(28) \\ a^3=512 \\ a=8 \end{gathered}`

Using this result, we can calculate b:

`b=(1152)/(a^2)=(1152)/(8^2)=(1152)/(64)=18`

Finally, the dimensions of the crate that will minimize the total cost of material are:

`8ft*8ft*18ft`