Question

Suppose that the weight in pounds of an airplane is a linear function of the amount of fuel in gallons in its tank. When carrying 10 gallons of fuel the airplane weighs 1955 pounds. When carrying 38 gallons of fuel it weighs 2109 pounds how much does the airplane weight if it’s carrying 56 gallons of fuel.

Answer 1

Since the weight and fuel have a linear relation, we can write it as

`y=mx+b`

where y denotes the weight in pounds and x the fuel in gallons.

We have 2 points of this linear relation, they are

`\begin{gathered} (x_1,y_1)=(10,1955) \\ \text{and} \\ (x_2,y_2)=(38,2109) \end{gathered}`

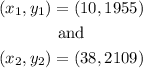
so the slope m from above is given as

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(2109-1955)/(38-10) \end{gathered}`

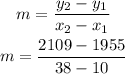
which gives

`\begin{gathered} m=(154)/(28) \\ m=5.5 \end{gathered}`

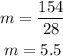
Then, the line equation has the form

`y=5.5x+b`

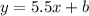
Now, we can find the y-intercept b by replacing one of the two given points, that is, if we substitute point (10,1955) into the last result, we get

`1955=5.5(10)+b`

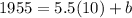
then, b is obtained as

`\begin{gathered} 1955=55+b \\ b=1955-55 \\ b=1900 \end{gathered}`

So, the line equation which model this problem is

`y=5.5x+1900`

Hence, by using this equation, we can find the weight of the airplane when the fuel is equal to 56 gallons, that is,

`y=5.5(56)+1900`

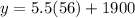
which gives

`\begin{gathered} y=308+1900 \\ y=1938 \end{gathered}`

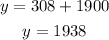
How much does the airplane weight if it’s carrying 56 gallons of fuel? 1938 pounds