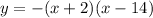Question

Nimo thought that the equationy=(x - 2)(x + 14) would match thegraph, but it didn't. Fix it, below!y = (x - 65)(x + 14)

Answer 1

In the given graph, the coordinates of the vertex of the parabola is,

(h, k)=(6, 64)

The given parabola is open downwards.

The vertex form of a parabola openingupwards or downwards is given by,

`y=a(x-h)^2+k\ldots\ldots(1)`

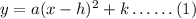
Here, a is a constant and (h, k) are the coordinates of the vertex of the parabola.

If a>0, parabola opens upwards and if a<0, theparabola opens downwards.

(x,y)=(14,0) is a point on the given parabola. So, put x=14, y=0 h=6 and k=64 in the above equation to find the value of a.

`\begin{gathered} 0=a(14-6)^2+64 \\ 0=a*8^2+64 \\ 0=a*64+64 \\ (-64)/(64)=a \\ -1=a \end{gathered}`

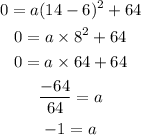
Now, put the values of a, h and k in equation (1).

`\begin{gathered} y=-1*(x-6)^2+64 \\ =-(x-6)^2+64 \end{gathered}`

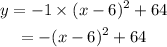
Now, rewriting the above equation,

`\begin{gathered} y=-(x^2-2*6x+6^2)+64^{} \\ =-(x^2-12x+36)+64 \\ =-x^2+12x-36+64 \\ =-x^2+12x+28 \\ =-(x^2-12x-28) \\ =-(x^2-14x+2x-14*2) \\ =-(x(x-14)+2(x-14)) \\ =-(x+2)(x-14) \end{gathered}`

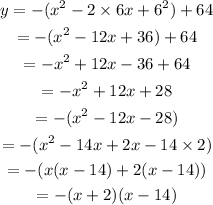
Therefore, the equation of parabola is,

`y=-(x+2)(x-14)`