Answer:
(1) The relationship between the altitude height, 'h', and the orbital speed,
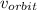 , of the satellite is an inverse relationship
, of the satellite is an inverse relationship
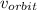 = 1/(h + R)
= 1/(h + R)
(2) The height of the satellite, is approximately 24,442 meters
(3) Please find attached the drawing showing the two lines that indicate the direction of the gravitational force on the satellites created with Microsoft Visio
Step-by-step explanation:
(1) From the given data table, as the altitude increases, the orbital velocity decreases, therefore, the relationship between altitude, 'h', and orbital velocity, '
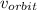 ', is an inverse relationship which can be expressed as follows;
', is an inverse relationship which can be expressed as follows;
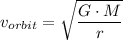
Where;
G = The universal gravitational constant
M = The mass of the Earth, or planet about which the satellite orbits
r = The distance between the center of the planet and the satellite = h + R
R = The radius of the planet
When
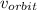 = 27,500, h = r - R = 1000
= 27,500, h = r - R = 1000
We have;
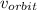 ² ∝ 1/r
² ∝ 1/r
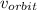 ² = k/r = k/(R+ h)
² = k/r = k/(R+ h)
When,
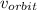 ² = 27,500² = 756,250,000
² = 27,500² = 756,250,000
r = h + R = 1000 + R
∴ 756,250,000 = k/(1000 + R)
(1,000 + R) × 756,250,000 = k
When,
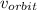 ² = 18,000² = 324,000,000
² = 18,000² = 324,000,000
r = h + R = 10,000 + R
∴ 324,000,000 = k/(10,000 + R)
324,000,000 = ((1,000 + R) × 756,250,000)/(10,000 + R)
∴ 324,000,000×(10,000 + R) = (1,000 + R) × 756,250,000
R × (756,250,000 - 324,000,000) = 324,000,000×10,000 - 1,000 × 756,250,000
R = (324,000,000×10,000 - 1,000 × 756,250,000)/(756,250,000 - 324,000,000) = 5746.09600925
R = 5,746.09600925
k = (1,000 + R) × 756,250,000 = (1,000 + 5,746.09600925) × 756,250,000 = 5.1017351 × 10¹²
k = 5.1017351 × 10¹²
(2) When,
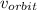 = 13,000 m/s, we have;
= 13,000 m/s, we have;
13,000² = 5.1017351 × 10¹²/(5,746.09600925 + h)
∴ 5,746.09600925 + h = 5.1017351 × 10^(12)/(13,000²) = 30187.7816568
h = 30187.7816568 - 5,746.09600925 = 24,441.6856476
The height of the satellite, h ≈ 24,442 meters
(3) Please find attached the drawing showing the two lines indicating the direction of the force of gravity exerts on the satellites created with Microsoft Visio.