Question

In the accompanying diagram of an isosceles triangle ABC, AB=~ AC, and exterior angle ACD=110. What is m

Answer 1

The triangle ABC is isoceles, this means that sides AB and AC are equal and the base angles

∠ABC and ∠BCA are equal.

The angle ∠BCA and the external angle ∠ACD are a linear pair, this means that they add up to 180º

From this we can calculate ∠BCA as

`\begin{gathered} \angle\text{BCA}+\angle\text{ACD}=180º \\ \angle\text{BCA}+110º=180º \\ \angle\text{BCA}=180º-110º \\ \angle\text{BCA}=70º \end{gathered}`

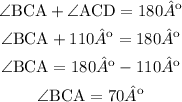
Since ∠BCA=∠ACB, then ∠ABC=70º

Now the sum of all interior angles of a triangle is equal to 180º so that

`\angle\text{ABC}+\angle\text{BCA}+\angle\text{BAC}=180º`

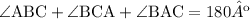
Since BCA and ACB are known we can unse this expression to calculate ∠BAC as follows

`\begin{gathered} 70+70+\angle\text{BAC}=180 \\ 140+\angle\text{BAC}=180 \\ \angle\text{BAC}=180-140 \\ \angle\text{BAC}=40 \end{gathered}`

m∠BAC=40º