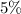Question

Ross has two bags. The first bag has six red, two silver, seven yellow and ten orange coins.The second bag contains four red, twelve silver, five yellow, and three orange coins. What isthe probability that he pulls an orange coin from both bags?

Answer 1

Step-by-step explanation:

The total number of coin in the first bag is given below as

`\begin{gathered} 6+2+7+10=25 \\ n(S)=25 \\ n(R)=6 \\ N(Si)=2 \\ n(O)=10 \end{gathered}`

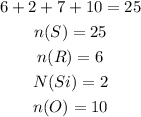
The probabaility of picking an orange ball from the first ba will b calcuated below as

`\begin{gathered} Pr(O)=(n(O))/(n(S)) \\ Pr(O)=(10)/(25)=(2)/(5) \end{gathered}`

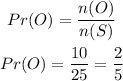
Step 2:

The total number of coin in the second bag is given below as

`\begin{gathered} 4+12+5+3=24 \\ n(S)=24 \\ n(R)=4 \\ n(Si)=12 \\ n(Y)=5 \\ n(O)=3 \end{gathered}`

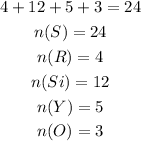
The probabaility of picking an orange ball from the second bag will be calcuated below as

`\begin{gathered} Pr(O)=(n(O))/(n(S)) \\ Pr(O)=(3)/(24)=(1)/(8) \end{gathered}`

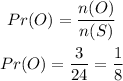
Hence,

The probabaility of picking an orange coin from both bags will be calculated below as

`\begin{gathered} Pr(O_1,O_2)=(2)/(5)*(1)/(8)=(2)/(40)=0.05 \\ Pr(O)=0.05*100=5\% \end{gathered}`

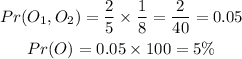
Hence,

The final answer is

`5\%`