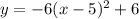The equation of a parabola in vertex form, is:
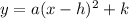
Where (h,k) are the coordinates of the vertex.
From the given graph, notice that the coordinates of the vertex are:
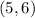
The roots are the values of x where the graph crosses the x-axis. In this case, the graph crosses the x-axis at the points (4,0) and (6,0). Then, the roots are:

Substitute the values of the vertex into the equation of the parabola in vertex form:
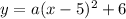
To find the value of a, substitute (x,y)=(4,0):
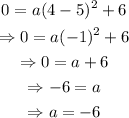
Therefore, the equation of the parabola is: