We are asked to find the limit of the following function.

As you can see, we cannot directly plug the value x = -4 into the function because it will make the denominator 0 and the function will be undefined.
First, we have to factor out the numerator.
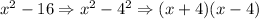
So, the function becomes

Finally, now we can plug the limit x = -4 into the above function

Therefore, the limit of the given function is equal to -8