Question

A rectangle of perimeter 100 units has the dimensions shown. Its area is given by the function A = w(50 - w). What is the GREATEST area such a rectangle can have?

The rectangle shown has 50-w on the top and bottom.
and a w on its left side and right side.

Answer 1

disregard the w and w-50 for now
to have the greatest area, try to make legnth and width the same
P=100
P=2(L+W)
100=2(L+W)
50=L+W
if L=W
50=L+L
divide 2
25=L=W

A=LW=25*25=625

greatest is 625 square units

Answer 2

The greatest area of rectangle is:

625 square units.

Explanation:

It is given that:

A rectangle of perimeter 100 units has the dimensions as:

50-w on the top and bottom.

and a w on its left side and right side.

i.e. we may say the length of the rectangle is:

50-w

and the width of the rectangle is:

w

Now, we need to find the greatest area of rectangle.

As the area of rectangle is:

A = w(50 - w)=50w-w^2

Now, to find the maximum area we differentiate the Area with respect to the width as:

`(dA)/(dw)=0\\\\i.e.\\\\50-2w=0\\\\50=2w\\\\w=25`

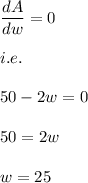
Hence, to obtain the maximum area the width of the rectangle is: 25 units.

and that of the length of the rectangle is:

50-25=25 units.

Hence, the dimensions of rectangle in order to obtain the maximum area is:

25 units by 25 units.

So, the area of rectangle is:

`Area=25* 25\\\\Area=625\ \text{square\ units}`

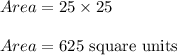
Hence, the greatest area of rectangle is:

625 square units.