Asymptotes.
A vertical asymptote is a vertical line near which the function grows without bound. In rational functions they can be identified as the poles of the functions, that is, the points where the denominator is zero AND the numerator is not zero.
A horizontal asymptote is a horizontal line to which the function gets very close as x grows without bonds. If the degree of the numerator and the degree of the denominator is equal, then the horizontal asymptote is calculated as the division of their leading coefficients.
We are given the function:
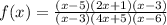
The denominator has a value of 0 if any of the factors is 0, that is when x=3, x=-5/4, or x=6.
But x=3 is also a root of the function, i.e., it makes the numerator as 0 also, so x=3 is not a valid vertical asymptote.
The vertical asymptotes are x=-5/4 and x=6.
The degree of the numerator is 3 and so is the degree of the denominator.
If we multiply the three leading coefficients of each binomial in the numerator we get 1*2*1 = 2.
If we do the same thing in the denominator we get 1*4*1 = 4. Thus the horizontal asymptote is y=2/4 = 1/2
Choice d. is correct