Question

Determine the value of x.Question options:A) 4.96B) 0.73C) 11.62D) 2.90

Answer 1

The question gives us a right-angled triangle with an opposite of x and an adjacent of 4. The angle of 71 degrees opposite the length x is also given. We are asked to find the value of x.

Step-by-step explanation

- The length x is the opposite because it is "opposite" the given angle. And this makes 4 the adjacent of the right-angled triangle.

- The question is easily solved by the SOHCAHTOA method. The opposite and adjacent are the variables in consideration, thus, TOA must be used from the SOHCAHTOA method.

- The TOA is defined as follows:

`\begin{gathered} \text{TOA:} \\ \tan \theta=\frac{\text{Opposite}}{\text{Adjacent}} \end{gathered}`

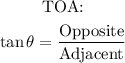
- With the above formula, we can proceed to solve the question as follows:

`\begin{gathered} \theta=71\degree \\ \text{Opposite}=x \\ \text{Adjacent}=4 \\ \\ \therefore\tan 71\degree=(x)/(4) \\ \\ \text{Cross multiply} \\ x=4\tan 71\degree \\ x\approx11.6168\approx11.62\text{ (To 2 decimal places)} \end{gathered}`

Final Answer

The value of x is 11.62 (OPTION C)